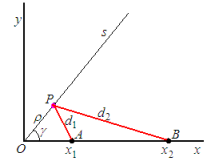
Calculates the minimum distance
"within (the sides of) an angle" (see Figure),
D = d1 + d2, to go from
A, with (fixed) x1 = 1, to
B, with x2, both on the x axis,
passing by P, to be determined, on the half-line s,
given the angle γ and x2. [γ :=
|MOD(γ, 90)| °.]
Point P = (x, y), with radial coordinate
ρ, is found by differentiation (D' = 0),
with solution x for
x−1 = ½
(x1−1 +
x2−1) sec²γ.
In polar coordinates, it is ρ =
2 R cos γ
(R below) and θ ≡ γ.
Counterintuitively, as γ → 0,
x tends to the harmonic (not the arithmetic) mean.
The extreme values for x and y
are, thus: 0 ≤ x ≤
2 x1 cos² γ ≤ 2 x1;
and 0 ≤ y ≤
x1 sin 2γ ≤
x1.
[Thus, the graph would not need to exceed (0, 0) to (2, 1).]
As γ varies, P describes a circle with
radius R centred at (R, 0), R =
x1x2 ⁄
(x1 + x2).
A graph is made as the one in the Figure. |
 |