1. Translações horizontais
CONTRAPONTO MUSICAL
Tradicionalmente, nas estruturas musicais distinguem-se: o ritmo, a melodia e a harmonia. O significado e a função de cada um destes elementos é facilmente perceptível para a maioria dos ouvintes, mesmo os menos dotados. No entanto, se este trio funciona bem para alguma música clássica, ele não serve para a chamada polifonia.
Foi sobretudo na Renascença que este género musical se desenvolveu. O seu princípio básico é o de que não deve existir apenas uma voz, mas sim um emaranhado de vozes. Essas vozes devem sobrepõem-se respeitando as leis da harmonia (cada voz sente-se acompanhada pelas restantes) segundo uma aprimorada arte canónica que se designa por contraponto. Tal como um ballet, há vozes que procedem em paralelo, outras que as seguem a curta distância e outras que se vão aproximando ou distanciando simetricamente do centro do palco. Embora a evolução dos gostos musicais não tenha favorecido o contraponto, existem alguns autores, como Bach, em que os detalhes contrapontísticos sobressaem sobre os demais ingredientes musicais.
Com a ajuda da linguagem e dos conceitos matemáticos consegue-se, com total transparência, descrever algumas práticas contrapontistas. Também através da geometria, com a qual se exercita a intuição visual, é possível compreender a música mesmo quando se trata de um ouvido menos dotado.
Visualização de uma Melodia
Sons e ruídos não são mais que perturbações da pressão do ar captadas pelo ouvido humano. Para os distinguir, e fazendo uma primeira aproximação diríamos que, num som musical, a perturbação é uma oscilação regular (tem um andamento sinusoidal) à qual se pode atribuir uma certa frequência (altura). Para simplificar, consideremos sons que tenham a mesma frequência e uma determinada duração, como por exemplo, quando se dedilha uma corda de uma guitarra ou se sopra no bocal de uma flauta. À sucessão destes sons que sucedem sem interrupções chamamos melodia. Assim, poderíamos representar uma melodia como uma função f(t) em que a frequência f depende do tempo t. Esta é uma função em escada porque a frequência é temporariamente constante, sendo o seu gráfico uma linha quebrada com traços horizontais e verticais. O ouvido humano, mesmo o menos dotado para a música, consegue reconhecer quando dois sons têm frequências uma o dobro da outra, ou seja, frequência f e 2f. Por exemplo, quando duas vozes, uma feminina e outra masculina se sobrepõem com agrado num coro, conseguem produzir uma sensação agradável (consonância), e pretendendo cantar a mesma melodia, geram de facto um grupo a função y = f(x), o outro y = 2 f(x). A duração dos sons associa-se geralmente a um múltiplo inteiro ou a uma fracção muito simples de uma certa unidade de tempo. Assim, um gráfico de uma melodia poder-se-à representar sobre uma quadrícula inteira: trata-se de uma linha quebrada que se pode sobrepor às linhas do papel quadriculado.
***
Numa tentativa de mostrar de que modo as transformações geométricas tiveram lugar nos aspectos estruturais musicais, iremos recorrer a alguns exemplos e à explicação clarificadora de Benedetto Sciemi(1999: 63-67):
"As próximas considerações referem-se à noção de gráfico de uma função f (escreve-se também y = f (x)), e que a variável x assume valores num determinado domínio, por exemplo no intervalo 0< x< 10.
O gráfico de f é uma linha particular, isto é, é o conjunto de pontos que têm coordenadas (x, f(x)) com x a variar no domínio. Se submetermos esta linha às transformações do nosso grupo musical observa-se que a nova figura é uma outra linha, que é também o gráfico de uma nova função estreitamente aparentada com a original. Precisamente, em correspondência com as quatro famílias principais, encontramos:
1. Translações horizontais |
ta: f(x) -> f(x-a)
2. Translações verticais |
nb: f(x) -> b+f(x)
3. Reflexões horizontais(=lago) |
ld:f(x) -> d-f(x)
4. Reflexões verticais(=muro) |
mc:f(x) ->f(c-x)
5. meias voltas(simetrias pontuais): |
gc,d: f(x) -> d-f(c-x)
O gráfico destas funções é, no essencial, redutível aos seguintes quatro casos particulares (todos os outros se obtêm transladando estes quadro):
f(x) -f(x) f(-x) -f(-x)
Eles podem ser ilustrados com o seguinte exemplo:
Efeito de quatro transformações sobre o gráfico de uma função.
Os quatro gráficos têm, como se vê, aspectos bem diferentes. Pelo contrário, o andamento das funções não é alterado pelas translações que se limitam a deslocar o gráfico (para cima ou para baixo, para a direita ou esquerda, ou ambas as direcções)."
 |
Passamos agora a apresentar alguns gráficos que representam excertos de composições musicais de J.S.Bach Estas pequenas ilustrações mostram como as transformações geométricas são importantes para a música. |
 |
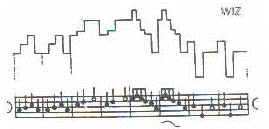
Exemplo 1: Translações Horizontais: |

Escrita tradicional e gráfico da melodia Fra Martino
Exemplo 2: Translações Verticais e Obliquas: |

Um autógrafo de J.S. Bach ( BWV 1073).
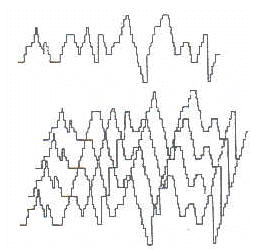
Realização gráfica do cânone BWV 1073
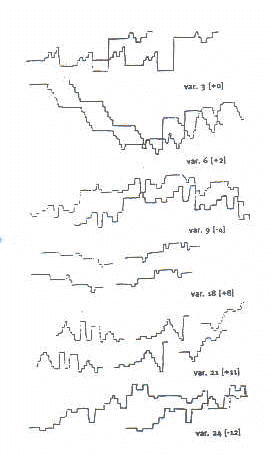
J.S. Bach: algumas das Variações Goldberg
Exemplo 3: Reflexões-lago: |

Efeito de uma reflexão lago no Fra Martino.
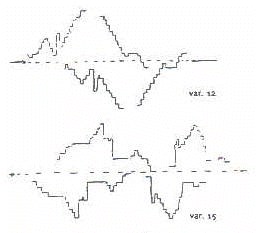
J.S. Bach: outras Variações Goldberg.
Exemplo 4: Reflexões- muro: |
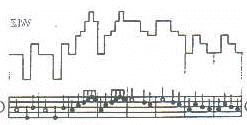
Efeito de uma reflexão- muro sobre Fra Martino
Exemplo 5: Outras transformações: |
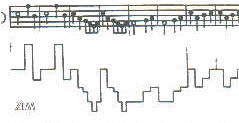
Efeito de uma meia volta em Fra Martino